Leaf Arrangement

Leaves nearly always appear singularly or paired. There’s nothing unusual about that, but the mathematics behind those arrangements may surprise you.

Take a look at a stem or flower from above. You will almost always see distinct patterns in the way the leaves and stems are organized. These patterns are called phyllotactic spirals. Very often, Fibonacci numbers and the Golden Mean (or Golden Angle) are involved. Fibonacci numbers are a big part of nature and architecture. You can get a simple explanation at the bottom of my post on garden design.

Echeveria

Leaf attachment

Leaves emerge along a twig or stem at points called nodes. The space between each node is called the internode. Sometimes, in the angled space between the leaf and the stem, called the leaf axil, a bud may appear. The scaly covering on buds is actually made up of modified leaves, called bud scales. Note that only leaf buds have scales; flower buds do not. Where leaves emerge, along a stem, is determined by plant hormones, called auxins.

Leaf arrangement

At the most basic level, leaves emerge from a stem either individually or in pairs. Leaves that take turns up a stem, alternating from one side to the other, are called alternate. Leaves that appear in pairs are called opposite. Leaves growing close to the ground, around an upright stem, whether alternate or opposite, are called basal. Leaves arranged like an upright deck of cards are called two-ranked, or distichous [dis-ti-kus].

Opposite leaf arrangement (McSush) CC BY-SA 3.0

Opposite leaf arrangements

Pairs of leaves can appear anywhere along a stem to be considered opposite. If opposite leaf pairs are successively positioned 90° apart along the stem, the arrangement is called decussate. This is a common growth habit of stone crops.

Alternate leaf arrangement (McSush) CC BY-SA 3.0

​Alternate leaf arrangements

Most of the time, alternate leaves take turns along the length of a stem, going from side to side. In some cases, such as magnolia, alternate leaves occur on all sides of a stem, in an apparent spiral. Closer inspection will show that it is not a true spiral. ​

When there are three or more alternate leaves growing in a true spiral, it is called a whorl. Whorls generally only occur in plants with very short internodes.

​Note: Trees almost never have a whorled leaf arrangement, white pine being the exception. Most often, trees produce short shoots, with clusters of leaves at the end. This is the normal leaf arrangement for apple, pear, and many other edible crop trees.

Spiral v. whorl (Roro) Public Domain

Basal leaf arrangements

When basal leaves are arranged in a whorl, it is called a rosette. Dandelion leaves are an example of rosette growth. Whorled leaves growing higher on a stem, in contrast, are said to be cauline.

Rosette dandelion leaves (Max Pixel) Public Domain

Distichous leaf arrangements
​
I like to think of the distichous arrangement as two ranks of leaves, standing on either side of the stem. Distichous leaves can be either alternate or opposite, depending on the species.

Distichous 'Clivia' (Narutodude000) CC BY 3.0

Leaf arrangement math

The fraction of a circle used to arrange leaves around a stem is very species specific. You don’t have to be a math whiz to understand this stuff, either. Let me explain:

•    Imagine a pie cut into 360 very skinny slices
•     Each slice is a degree (°)
•     If you take 1/4 of the pie, you would have 90 slices or 90°  [360/4 = 90]
•     If you take 1/3 of the pie, you would have 120° [360/3 = 120]

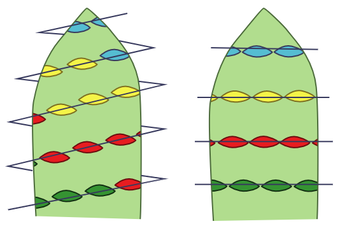
Now look at leaf arrangement along and around a stem in the same way:

•     If a plant uses four leaves to go around a stem, each leaf is 90° apart
•     If a plant uses three leaves to go around a stem, each leaf is 120° apart

Are you with me? Hang in there! This stuff is amazing!

So, since leaves and stems are different sizes, and species have different sunlight needs, there are different fractions, or ratios of rotation, around a stem. For example, hazel leaves are arranged in 1/3 (or 120°) rotations, apricots use 2/5 rotations, sunflowers and pears use 3/8, and almonds use 5/13. This means that the leaves of an almond tree are positioned 5/13th of the pie apart. If you do the math, this works out to 38.5° between each leaf attachment, as you work your way up or down a stem.

This is where it gets really weird!

The fractions that describe leaf arrangement are almost always made with a Fibonacci number and its successor, as the numerator and denominator, respectively. Now, the number of steps taken for a leaf arrangement to work its way around a stem, before repeating the pattern, is called its gyres. A three leaf cycle of rotation has one gyre, while a five leaf cycle takes 2 gyres. The number of gyres ends up being the numerator in the Fibonacci number that describes the rotation! Holy spring bulbs, Birdman!

Whorls take this math to a whole new level

The rotation of successive whorls is nearly always one-half the angle between the leaves. For example, say you have a whorled leaf arrangement that uses three leaves. From what we calculated above, there would be 120° between each of those leaves, along the length of the stem. All the other whorls will be half that distance, or 60° apart from each other. I have no idea why.

Bottom line: whether leaves are alternate, opposite, whorled, basal, or distichous, the mathematics of leaf arrangement ends up providing each leaf with the optimal amount of sunlight.

[If you really love this stuff, check out Gray’s Botanical Textbook: Structural Botany (1879)]